“O grande livro do Universo está escrito em linguagem Matemática.” (Galileu)
"A onipresença do PHI na natureza, disse Langdom claramente está além da coincidência, e assim os antigos presumiram que o número PHI deve ter sido predeterminado pelo Criador do universo. Os primeiros cientistas solenemente anunciavam que o número era a Divina Proporção."
“O número de ouro rege a Natureza”.
O abacaxi é uma fruta saudável e de sabor agradável. Ele é considerado o rei dos frutos, por ser muito belo e portar uma coroa em seu cume.
Quem já parou um momento para observar o design do abacaxi deve ter notado a sua beleza... Sua casca (malha) é formada por espirais. Sendo 8 espirais para a direita e 13 para a esquerda.
Por que os números 8 e 13?
Sabe-se apenas que esses números fazem parte de uma sequência numérica muito encontrada na natureza e que ficou conhecida como os números de Fibonacci. Os números são:
Sabe-se apenas que esses números fazem parte de uma sequência numérica muito encontrada na natureza e que ficou conhecida como os números de Fibonacci. Os números são:
0, 1. 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765,10946...
Consiste numa sucessão de números, tais que, definindo os dois primeiros como sendo 1, os seguintes são obtidos através da soma dos seus dois antecessores.
O rácio de Fibonacci foi descoberto por Leonardo de Pisa, também conhecido por Fibonacci por volta do ano 1200. Fibonacci apercebeu-se que existia um rácio matemático absoluto que surgia muitas vezes na natureza, uma espécie de ordem universal que desenha a natureza e que propicia ao olho humano naturalidade, equilíbrio e beleza.
O rácio de Fibonacci foi descoberto por Leonardo de Pisa, também conhecido por Fibonacci por volta do ano 1200. Fibonacci apercebeu-se que existia um rácio matemático absoluto que surgia muitas vezes na natureza, uma espécie de ordem universal que desenha a natureza e que propicia ao olho humano naturalidade, equilíbrio e beleza.
Leonardo de Pisa, descobriu esta sequência resolvendo um problema relativo ao crescimento de uma população de coelhos.
Dessa sequência, extraí-se o número transcendental conhecido matematicamente como Phi (1,618)
O Número de Ouro é aproximado pela divisão do enésimo termo da Série de Fibonacci e também é chamado de Proporção Áurea, Número Áureo, Proporção Dourada, Segmento Áureo, Divina Preoporção e etc.
Dessa sequência, extraí-se o número transcendental conhecido matematicamente como Phi (1,618)
O Número de Ouro é aproximado pela divisão do enésimo termo da Série de Fibonacci e também é chamado de Proporção Áurea, Número Áureo, Proporção Dourada, Segmento Áureo, Divina Preoporção e etc.
Trata-se de uma constante real algébrica irracional representada pela letra grega Φ (PHI), em homenagem ao escultor Phideas (Fídias), que a teria utilizado para conceber o Partheonon. O Número de Ouro é misterioso enigmático se apresenta na forma de uma razão, sendo considerado por muitos como uma oferta de Deus ao mundo.
Seu valor arredondado é 1,618.
A Proporção Áurea aparece no comportamento da refração da luz, dos átomos, no canto das baleias, nos marfins dos elefantes, nas plantas, na proporção das conchas do caramujo marinho Nautilus, nas ondas no oceano, nos furacões, nas espirais das galáxiass, no corpo dos seres humanos (o tamanho das falanges, ossos dos dedos por exemplo) entre inúmeros outros exemplos que envolvem a ordem do crescimento. O fascínio pelo Número de ouro data de há mais de 2 000 anos Os "antigos" aperceberam-se que a arte e a arquitetura baseadas na Razão de Ouro, eram harmoniosas e muito agradáveis à vista.
A Proporção Áurea aparece no comportamento da refração da luz, dos átomos, no canto das baleias, nos marfins dos elefantes, nas plantas, na proporção das conchas do caramujo marinho Nautilus, nas ondas no oceano, nos furacões, nas espirais das galáxiass, no corpo dos seres humanos (o tamanho das falanges, ossos dos dedos por exemplo) entre inúmeros outros exemplos que envolvem a ordem do crescimento. O fascínio pelo Número de ouro data de há mais de 2 000 anos Os "antigos" aperceberam-se que a arte e a arquitetura baseadas na Razão de Ouro, eram harmoniosas e muito agradáveis à vista.
Em uma rosa, a ocorrência do Número de Ouro pode ser notada na disposição de suas pétalas. Elas separam-se por ângulos que são frações de Φ (Phi). Essa disposição permite arranjar as pétalas de forma compacta e maximizar a sua exposição à luz
Alguns exemplos de plantas onde se encontra os números de Fibonacci.
3 pétalas: lírio, açucena, íris, trandescância.
5 pétalas: botão de ouro, rosa selvagem, columbine, esporas, capuchinha.
8 pétalas: delphiniums, anémona.
13 pétalas: malmequer, cineraria, ragwort.
21 pétalas: áster, olhado preto, susana, chicória.
34 pétalas: tanchagem, píretro, dália.
55,89 pétalas: margaridas (várias), a família asteraceae.
Algumas destas flores têm mesmo este número preciso de pétalas, outras podem variar, mas sempre com um número de pétalas, perto do de Fibonacci.etc...
Os arranjos das folhas de algumas plantas em torno do caule são números de Fibonacci. Com este arranjo, todas as folhas conseguem apanhar os raios solares de igual forma. Quando chove, o escoamento da água torna-se também mais fácil.
Desde a Antiguidade a Proporção Aurea é empregada na arte. É frequente sua incidência em pinturas renascentistas principalmente em obras de Leonardo Da Vinci (A Monalisa é um exemplo)..
O homem descrito por Vitrúvio apresenta-se como um modelo ideal para o ser humano, cujas proporções são perfeitas, segundo o ideal clássico de beleza. (Desenho de Leonardo da Vinci)
Uma construção geométrica muito famosa é a do chamado Retângulo de
Ouro. É o retângulo que quando é dividido em duas partes e em que uma dessas partes seja um quadrado, então o que resta terá que ser um retângulo com as mesmas proporções do retângulo inicial.
Trata-se do retângulo no qual a proporção entre o comprimento e a largura é aproximadamente o número Φ (Phi) ou seja, 1,618.
Muitos testes psicológicos evidenciaram que o Retângulo de Ouro é um dos retângulos mais agradáveis à vista humana.
O número de ouro pode ser encontrado através da razão da largura e do comprimento de um retângulo de ouro.
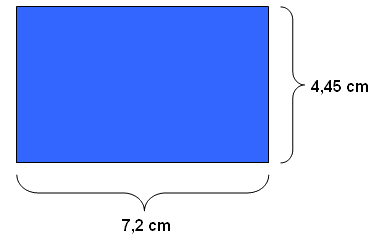
Se dividirmos a largura pela altura (o lado maior pelo menor), obteremos aproximadamente 1,618 que é a Razão Áurea”. Diversas pesquisas demonstraram que é a forma geométrica mais agradável aos olhos humanos. Por isso, esse formato é adotado em livros, quadros e construções.
Esta figura mostra, como se pode desenhar uma espiral, unindo quartos de círculos em cada novo quadrado (inscrito no rectângulo de ouro). A espiral obtida é conhecida como a espiral de Fibonacci.
Semente de girassol – A proporção em que aumenta o diâmetro das espirais de sementes de um girassol é a razão áurea.
O centro é marcando com um ponto. Pode-se ver que as sementes parecem formar espirais a curvar tanto para a direita como para a esquerda. Se contar essas espirais que partem da direita, a partir da borda da figura, são 34. Para o outro lado quantas são? Verá que esses dois números são vizinhos na série de Fibonacci.
Concha do Nautilus
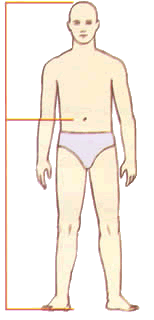
Corpo humano
A linha dos olhos marca uma divisão áurea em relação ao comprimento total do rosto e também existe proporção áurea da distância entre a base do nariz e a extremidade do queixo.
O resultado da divisão da altura de uma pessoa distância entre seu umbigo e o chão é o número áureo Phi = 1,618 aproximadamente.
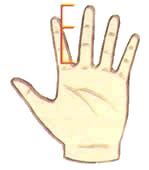
O tamanho dos dedos tem proporções áureas com cada uma de suas articulações.
O Número de Ouro fascinou os matemáticos pela sua extraordinária presença
nas várias facetas da Natureza
Atualmente, essa proporção ainda é muito usada. Ao padronizar internacionalmente algumas medidas usadas em nosso dia-a-dia, os projetistas procuraram "respeitar" a proporção divina. A razão entre o comprimento e a largura de um cartão de crédito, alguns livros, jornais, uma foto revelada, entre outros.
Série de Fibonacci
A a razão é 1,618 a partir do 10º termo da série
Razão = Número / Número anterior
...
89 1,61818181818182
144 / 89 =
144 1,61797752808989
233 1,61805555555556
377 1,61802575107296
610 1,61803713527851
987 1,61803278688525
1597 1,61803444782168
2584 1,61803381340013
...
número phi= 1,61803 39887...
Série de Fibonacci
Cada termo é a soma dos dois anteriores
0, 1. 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765,10946...
89 + 144 = 233

















Bom
ResponderExcluir